算BaTiO3的极化
\(P_z = 0.243230914 \text{ C/m}^{-2}\) \(\Delta E=5.309 \text{meV}\) 数据下载链接
ToC
1. 收敛测试
SYSTEM = BaTiO3 pm-3m ISTART = 0 ICHARG = 2 ENCUT = 525 EDIFF = 1E-6 ISMEAR = 0; SIGMA = 0.05 GGA = PS LREAL=.FALSE. LWAVE=.FALSE. LCHARG=.FALSE. NCORE = 4
BaTiO3 pm-3m 1 4.0 0.0 0.0 0.0 4.0 0.0 0.0 0.0 4.0 Ba Ti O 1 1 3 D 0.0 0.0 0.0 0.5 0.5 0.5 0.5 0.5 0.0 0.5 0.0 0.5 0.0 0.5 0.5
Auto 0 G 6 6 6 0 0 0
在INCAR中加了GGA = PS是因为看到了这段话:“In the present study, we have shown that the use of the novel PBEsol and HSE functionals gives a significant improvement of the description of the ABO3 perovskites SrTiO3 and BaTiO3 in their cubic and tetragonal phases.”1
测试情况如下:
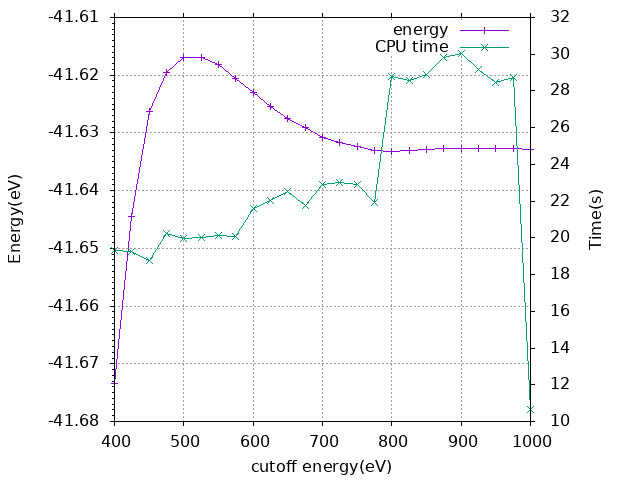
取ENCUT = 750即可。
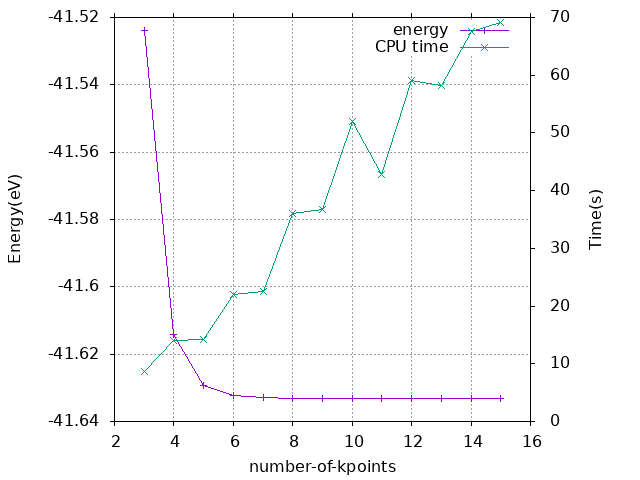
k点大小取6x6x6。
2. 结构优化
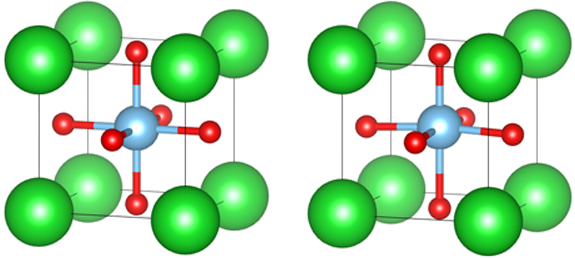
INCAR设置了ISIF = 3,进行自动优化,结果如下图,左边是立方的,右边是正方的:
具体参数如下。
cubic 对称相
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
SYSTEM = BaTiO3 pm-3m
ISTART = 0
ICHARG = 2
ENCUT = 750
EDIFF = 1E-6
ISMEAR = 0; SIGMA = 0.05
ISIF = 3
EDIFFG = -0.005
IBRION = 2
NSW = 50
POTIM = 0.1
GGA = PS
LREAL=.FALSE.
LWAVE=.FALSE.
LCHARG=.FALSE.
初始和自动优化得到的结构如下:
BaTiO3 pm-3m 1 4.0 0.0 0.0 0.0 4.0 0.0 0.0 0.0 4.0 Ba Ti O 1 1 3 D 0.0 0.0 0.0 0.5 0.5 0.5 0.5 0.5 0.0 0.5 0.0 0.5 0.0 0.5 0.5
BaTiO3 pm-3m
1.00000000000000
3.9900974324714453 -0.0000000000000000 -0.0000000000000000
-0.0000000000000000 3.9900974324714453 -0.0000000000000000
0.0000000000000000 0.0000000000000000 3.9900974324714453
Ba Ti O
1 1 3
Direct
0.0000000000000000 0.0000000000000000 0.0000000000000000
0.5000000000000000 0.5000000000000000 0.5000000000000000
0.5000000000000000 0.5000000000000000 0.0000000000000000
0.5000000000000000 0.0000000000000000 0.5000000000000000
0.0000000000000000 0.5000000000000000 0.5000000000000000
tetragonal 铁电相
INCAR和KPOINTS和POTCAR都和刚才Cubic的一样,初始位置把Ti原子移动了1%的z边长。初始和自动优化得到的结构如下:
BaTiO3 p4mm 1 4.0 0.0 0.0 0.0 4.0 0.0 0.0 0.0 4.0 Ba Ti O 1 1 3 D 0.0 0.0 0.0 0.5 0.5 0.51 0.5 0.5 0.0 0.0 0.5 0.5 0.5 0.0 0.5
BaTiO3 p4mm
1.00000000000000
3.9825948945145262 -0.0000000000000000 -0.0000000000000000
-0.0000000000000000 3.9825948945145262 0.0000000000000000
-0.0000000000000000 0.0000000000000000 4.0297206870837838
Ba Ti O
1 1 3
Direct
-0.0000000000000000 0.0000000000000000 0.0084659470882332
0.5000000000000000 0.5000000000000000 0.5200611024005698
0.5000000000000000 0.5000000000000000 -0.0102081651767469
0.0000000000000000 0.5000000000000000 0.4958405578439712
0.5000000000000000 -0.0000000000000000 0.4958405578439712
3. 铁电极化
Remember that the number that you have now calculated is the absolute value of the polarization, and is only defined modulo a polarization quantum. To calculate the spontaneous polarization in a ferroelectric for example, the procedure should be repeated also for a high symmetry, non-polar reference state. The difference between the two values, taken along the same branch of the polarization lattice, is then the spontaneous polarization. Sometimes it is necessary to re-calculate the polarization for a number of structures along the deformation path between the high- and low-symmetry structures in order to know unambiguously which difference to take.2
结合这篇2和官网的介绍,对Berry Phase Method的大概理解:
- relax high symmetry non-polar structure (reference) and low symmetry polar phase (target) using VASP
- create several structures along the deformation path between the high and low symmetry structures
- run Berry phase method calculations for each structures using VASP
- find polarization branches by adding integer number times of polarization quantum
- spotaneuous polarization is the difference along the same branch between reference and target
第二步创建中间的结构的时候,用了Vtst Scripts里面的nebmake.pl脚本。
第三步的INCAR加上了DIPOL和LCALCPOL标签,并且自洽计算,不动原子:
1
2
3
4
5
6
7
8
9
10
11
12
SYSTEM = BaTiO3
ISTART = 0
ICHARG = 2
ENCUT = 750
EDIFF = 1E-6
ISMEAR = 0; SIGMA = 0.05
LCALCPOL = .TRUE.
DIPOL = 0.5 0.5 0.5
GGA = PS
LREAL=.FALSE.
LWAVE=.FALSE.
LCHARG=.FALSE.
相应的OUTCAR的解释在官网这里,把p[ion]和p[elc]加起来得到xyz三个方向的总dipole moment,记为\(p\),z方向的记为\(p_z\)。
在第四步,由于首尾的立方和四方结构的晶矢不一样,所有创建的结构的晶胞大小、极化量子都不一样。如果用电子电荷乘z方向格矢c的长度除以对应结构的晶胞大小作为z方向极化量子(\(\frac{eR}{V}\)),那么会导致整数倍加减极化量子之后,在第五步不同branch算出来的spotaneous polarization并不相同,不符合定义。因此下面尝试了两种思路进行处理:
方法一:拟合曲线找branch
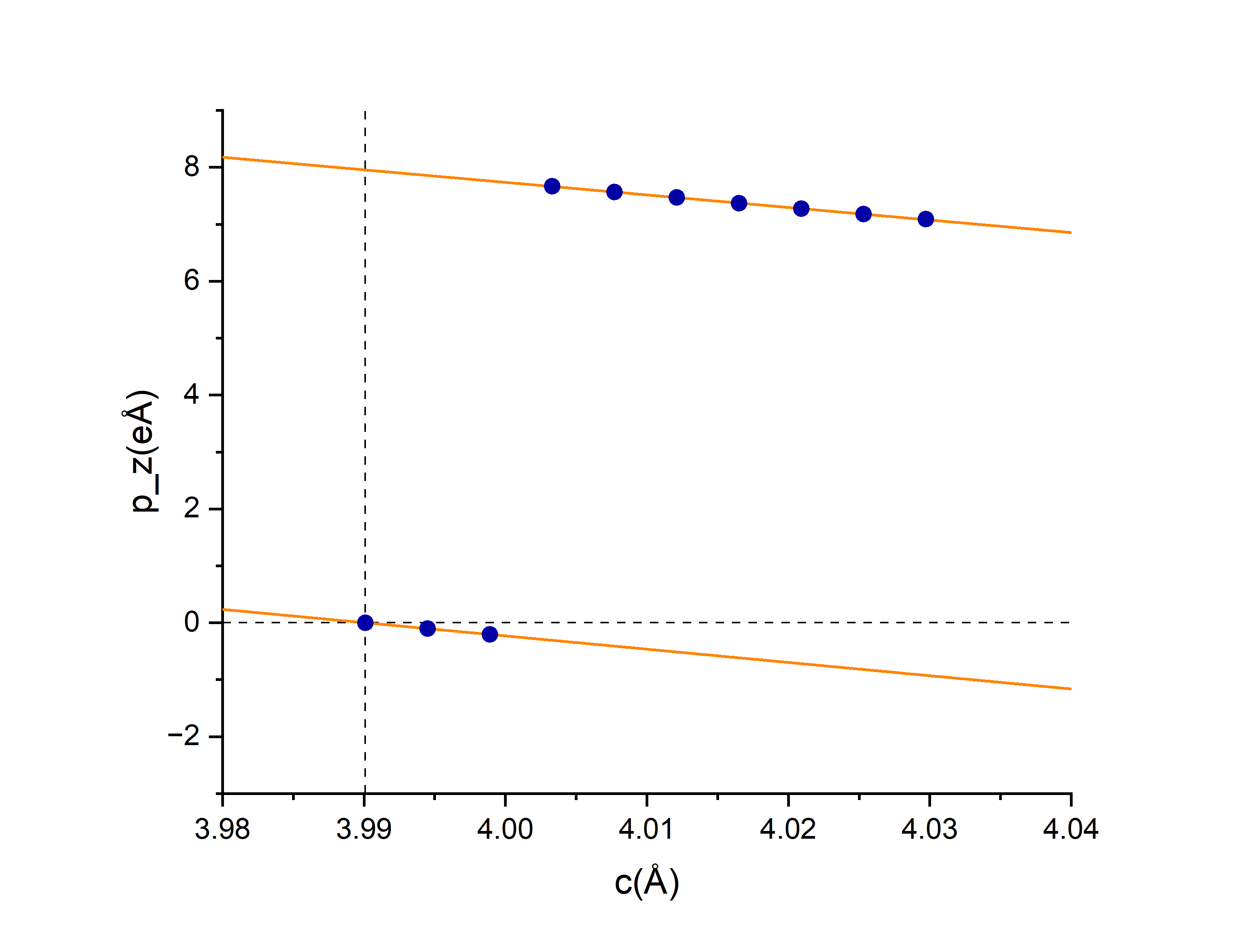
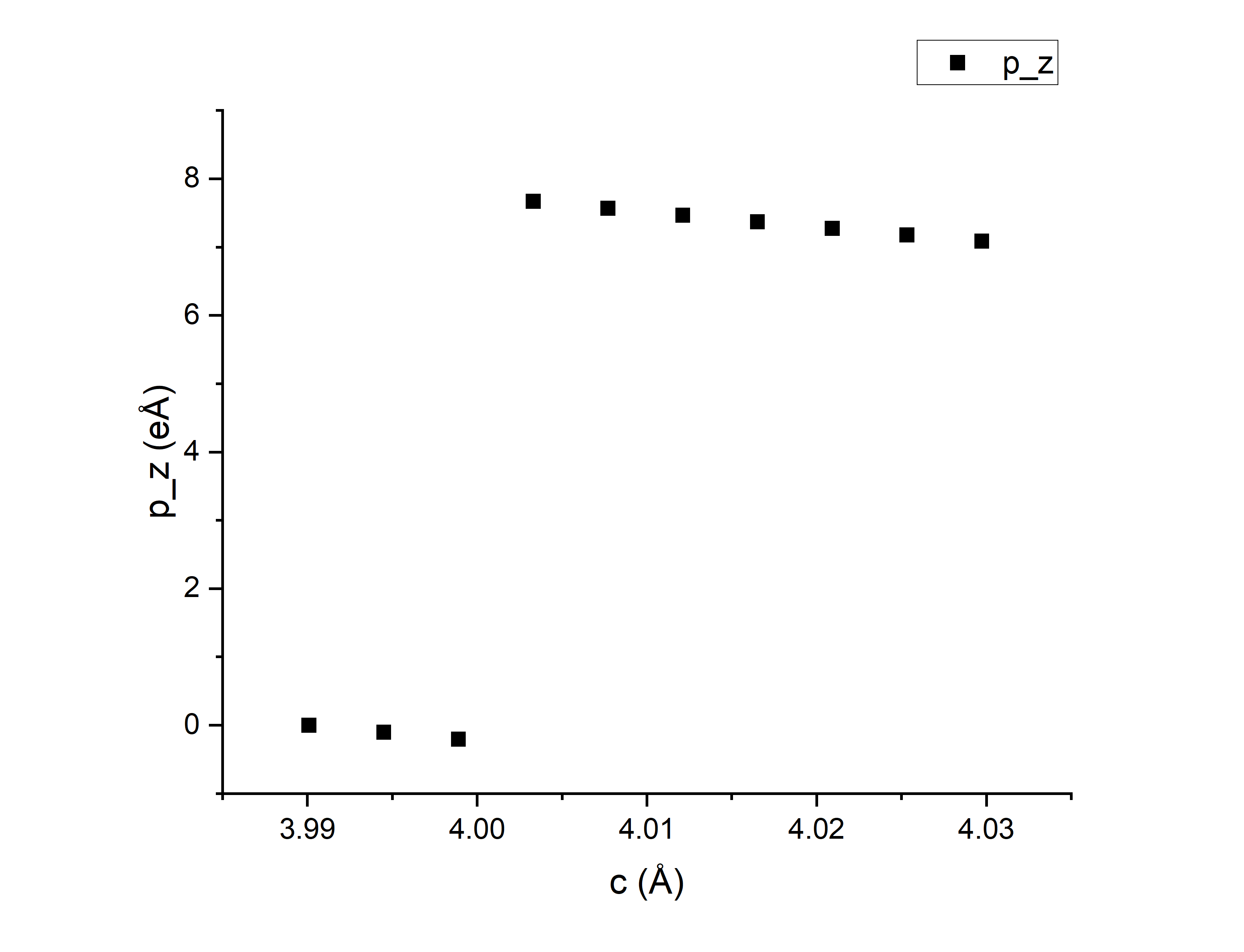 在第二步的时候在cubic和tetragonal(Ti向上)之间创建了8个中间过渡结构,第三步计算完之后得到\(p_z\),用z方向格矢长度c标记了cubic、中间8个、tetra总共10个结构,把每个结构的\(p_z\)画在图上,图上最左边第一个点是没有极化的cubic结构,越往右的点格矢c越长、极化越大,最右边是极化最大的tetra结构。可以看到,由于选的DIPOL参考点不是很巧,前三个结构和后七个结构算的结果并不在同一支上。
用后七个点拟合出一条\(p_z(c)\)函数,从第一个点作垂线,计算交点和第十个点的纵坐标差值记为\(\Delta p_z\),除以立方结构的晶胞大小得到极化值。
在第二步的时候在cubic和tetragonal(Ti向上)之间创建了8个中间过渡结构,第三步计算完之后得到\(p_z\),用z方向格矢长度c标记了cubic、中间8个、tetra总共10个结构,把每个结构的\(p_z\)画在图上,图上最左边第一个点是没有极化的cubic结构,越往右的点格矢c越长、极化越大,最右边是极化最大的tetra结构。可以看到,由于选的DIPOL参考点不是很巧,前三个结构和后七个结构算的结果并不在同一支上。
用后七个点拟合出一条\(p_z(c)\)函数,从第一个点作垂线,计算交点和第十个点的纵坐标差值记为\(\Delta p_z\),除以立方结构的晶胞大小得到极化值。
方法二:固定晶矢
为了避免第二步以后晶格不相同的计算问题,在第一步选择创建两个晶格一样、但极化方向相反的结构。在结构优化的时候得到了Ti向上的,将这个结构稍微修改(保持晶格大小,Ti初始往下移动1%)作为POSCAR,INCAR设置只移动原子的ISIF=2自动优化,得到的CONTCAR如下:
BaTiO3 p4mm 1 4.0 0.0 0.0 0.0 4.0 0.0 0.0 0.0 4.0 Ba Ti O 1 1 3 D 0.0 0.0 0.0 0.5 0.5 0.51 0.5 0.5 0.0 0.0 0.5 0.5 0.5 0.0 0.5
SYSTEM = BaTiO3 p4mm ISTART = 0 ICHARG = 2 ENCUT = 750 EDIFF = 1E-6 ISMEAR = 0; SIGMA = 0.05 ISIF = 2 EDIFFG = -0.001 IBRION = 2 NSW = 80 POTIM = 0.1 GGA = PS LREAL=.FALSE. LWAVE=.FALSE. LCHARG=.FALSE.
BaTiO3 p4mm
1.00000000000000
3.9825948945145262 -0.0000000000000000 -0.0000000000000000
-0.0000000000000000 3.9825948945145262 0.0000000000000000
-0.0000000000000000 0.0000000000000000 4.0297206870837838
Ba Ti O
1 1 3
Direct
-0.0000000000000000 0.0000000000000000 0.0084659470882332
0.5000000000000000 0.5000000000000000 0.5200611024005698
0.5000000000000000 0.5000000000000000 -0.0102081651767469
0.0000000000000000 0.5000000000000000 0.4958405578439712
0.5000000000000000 -0.0000000000000000 0.4958405578439712
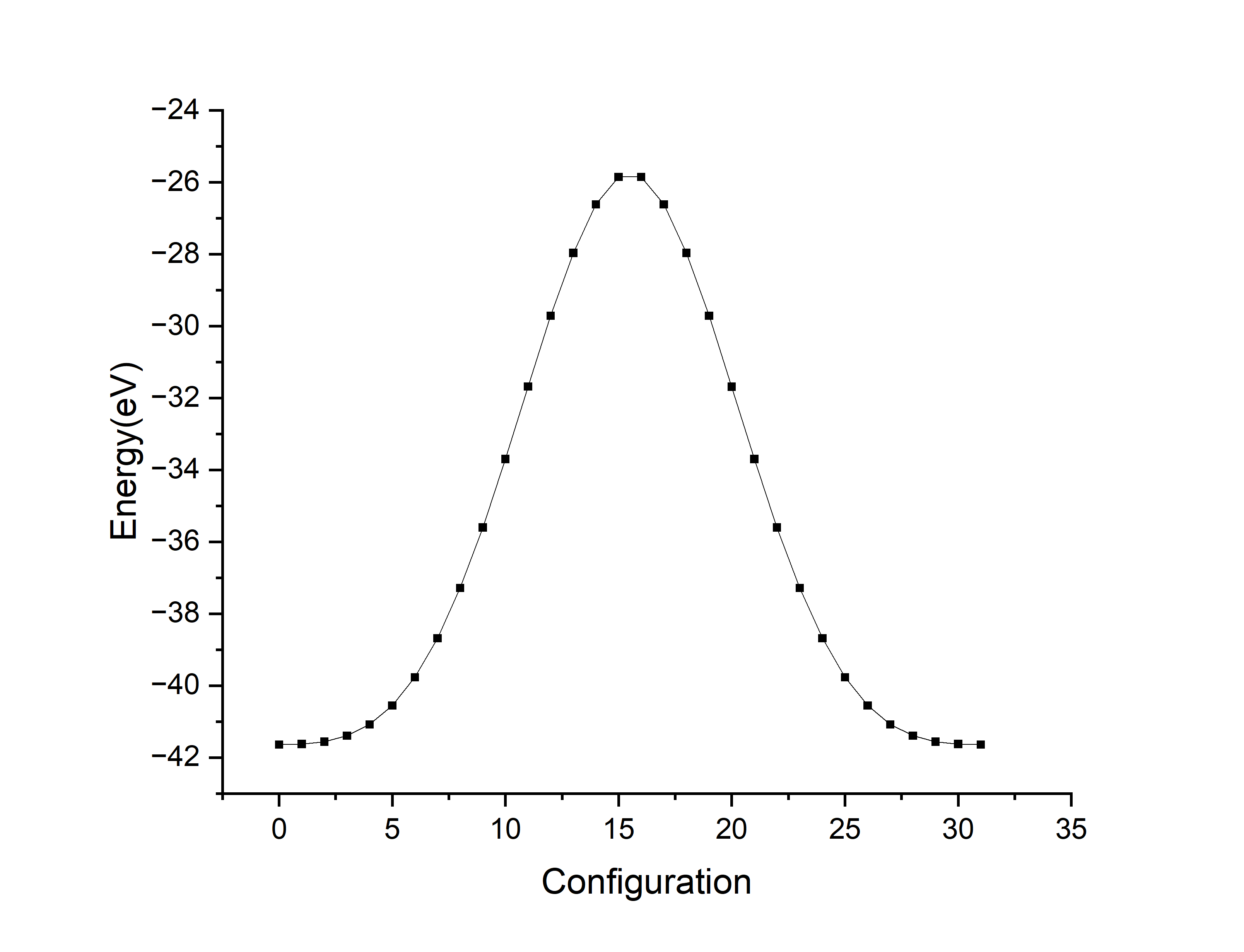
第二步的时候在Ti向下(编号00)和Ti向上(编号32)的两种极化方向之间创造了30个中间过渡结构,一共32个结构。第三步的berry phase计算INCAR参数和方法一相同,处理OUTCAR得到\(E\)和\(p_z\)。其中,第15和16个结构没有极化(vasp没有算出dipole moment结果),第15个的能量比第16个稍高。作图如下:
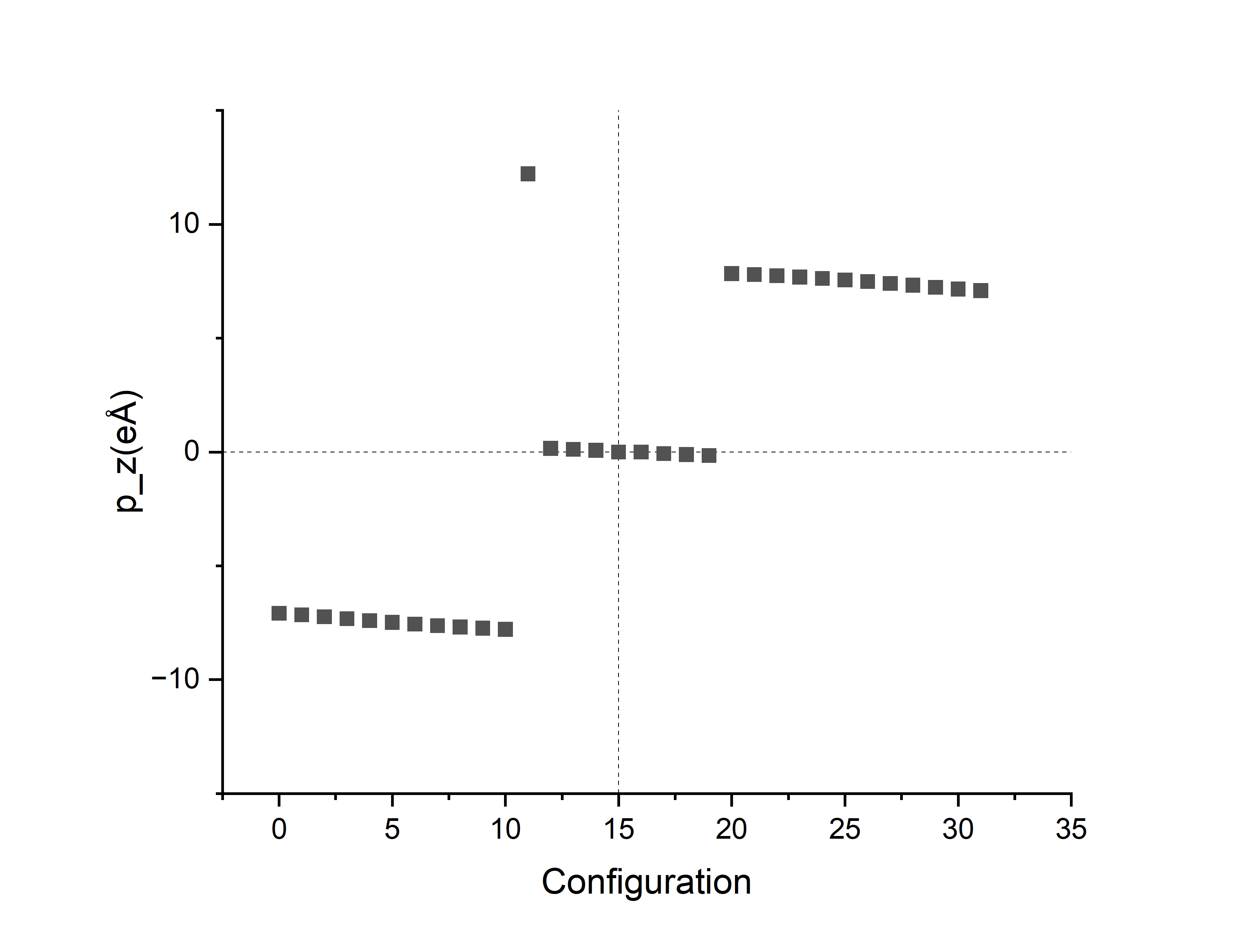
由于DIPOL参考点不够凑巧,32个点分布在4支上。接下来对这4个branch进行处理:
由于对极化\(P\)加减整数倍极化量子\(\frac{eR}{V}\)就相当于对dipole moment \(p\)加减整数倍\(eR\),由于\(p_z\)一开始取了单位\(\text{ e}\mathring{A}\),只要加减整数倍的z方向格矢长度\(R_z=c\)即可,即:将上图的\(p_z\)点整体向上向下平移格矢c的整数倍距离:
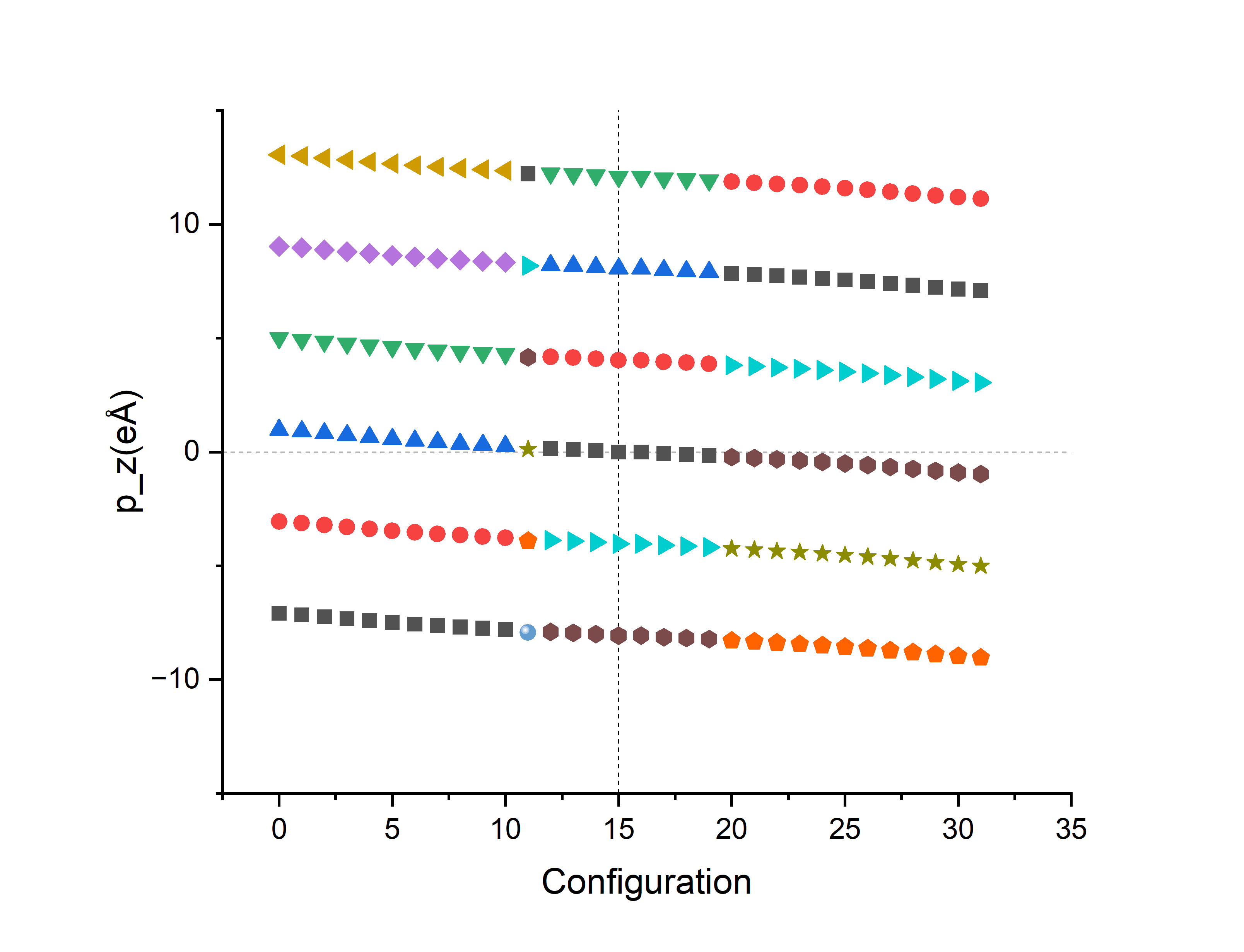
可以初见4个branch的雏形,将其连线,每条线最左边的点和最右边的点的差值即为2倍的\(\Delta p_z\)(因为这是相反极化方向之间的差值,所以是2倍)。
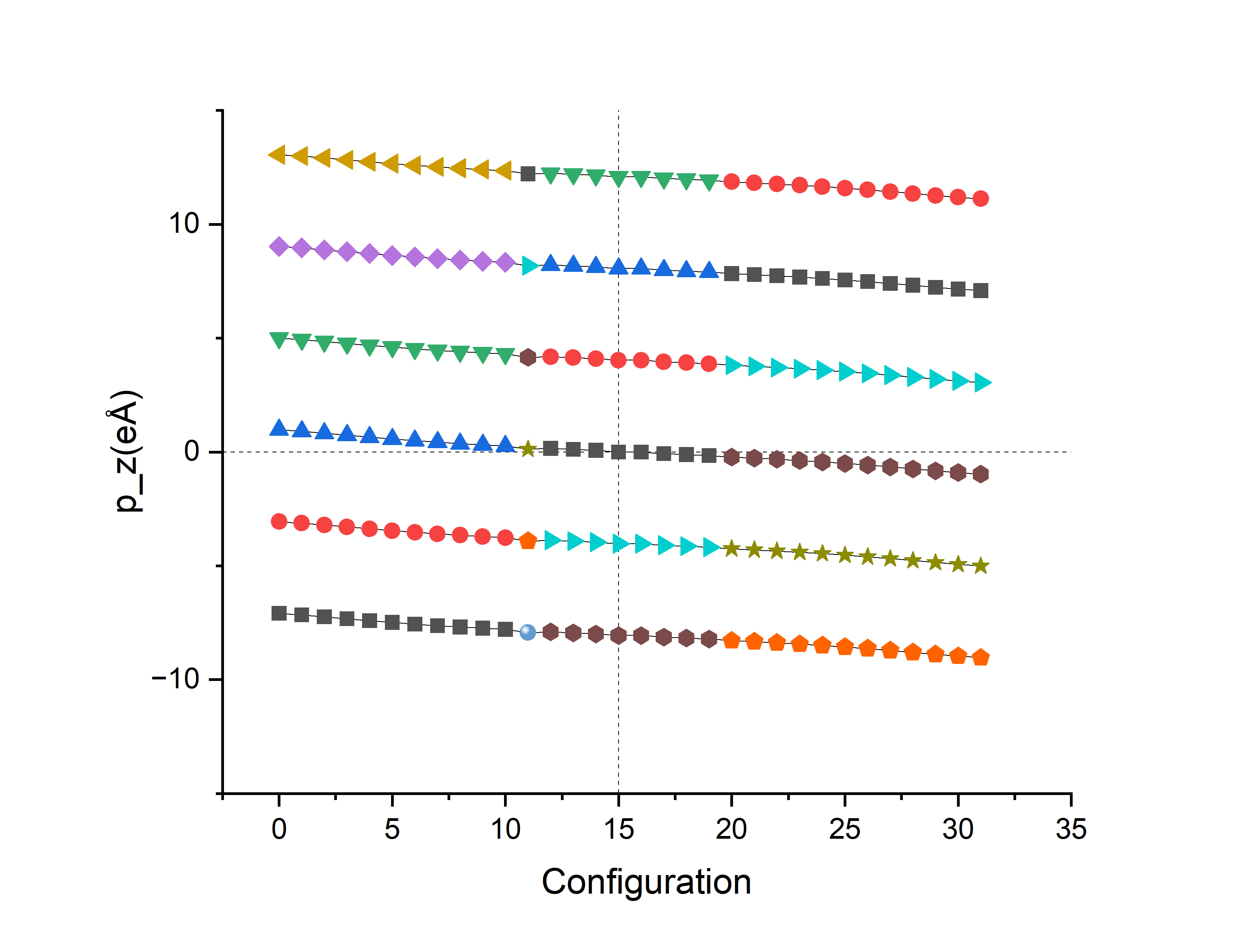
算得极化值约为\(0.24\text{ Cm}^{-2}\),实验3是\(0.26\text{ Cm}^{-2}\),相差8%。
4. 翻转能垒
看了这篇的图片之后大概知道要在可能的路径上插入中间态结构算出每个路径的势垒曲线,但因为BaTiO3极化翻转的路径比较简单,直接用对称相能量减去铁电相的能量:\(\Delta E=-41.633588+41.638897 \text{eV}=5.309 \text{meV}\)
5. 问题
- 还是不知道到底应该怎么算铁电极化:如果按照方法一处理,万一不是直线,拟合就没用了;如果按照方法二处理,其中的应该视为对称相的那个晶胞是拉长的,在vesta里看了一下并不是对称的,感觉不符合实际,路径也不符合实际,算出来的势垒也和优化过结构的对称相与铁电相的差值不相等。
6. 反馈
采用方法二。对4条branch进行修正获得一条连续极化曲线就能得到真正的极化值了,一般直接取中间PE相极化值过零点的连续曲线,用+P或者-P对应的极化值就可以得到δP了(就是你上面说的进行整数倍极化量子数修正)。通过修正极化量子数,得到一条极化值随位移的连续曲线,就可以按照你后续操作获得FE的极化值了。FE和PE相要直接相减的话,结构框架(晶格参数)应该是一致的才行,PE相的时候直接拉长极化轴(c轴),晶体对称性应该不会变,除非拉长后又优化了(也就是说中间插点的结构不要优化),。
-
J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou, and K. Burke, Restoring the ensity-Gradient Expansion for Exchange in Solids and Surfaces, Phys. Rev. Lett. 100, 136406 (2008) ↩
-
N. A. Spaldin, A beginner’s guide to the modern theory of polarization, Journal of Solid State Chemistry 195, 2 (2012). ↩ ↩2
-
R. Imura, Y. Kitanaka, T. Oguchi, Y. Noguchi, and M. Miyayama, Spontaneous Polarization and Local Structures in Ca-substituted BaTiO3, Trans. Mat. Res. Soc. Japan 39, 121 (2014). ↩